Capítulo 1 del curso

Estimación histograma de la densidad

La idea es que una variable aleatoria tiene un proceso o función de densidad subyacente la cuál genera los datos que tendremos finalmente a disposición. Dada una variable aleatoria $X$, entonces $X \sim f\left(x;\theta\right)$. En el caso paramétrico la estimación de la función de densidad estaría dada por $\hat f \left(x;\theta\right) = f\left(x;\hat{\theta}\right)$ asumiendo que la población de la cuál provienen los datos sigue una distribución conocida con función de densidad $f$.

En el caso no paramétrico, no se hace supuesto alguno sobre la función de densidad asociada a la población de la cuál provienen los datos. La estimación de la función de densidad puede hacerse por diferentes métodos, entre ellos los siguientes:

Histograma
Polígono de frecuencias
Núcleo (kernel)

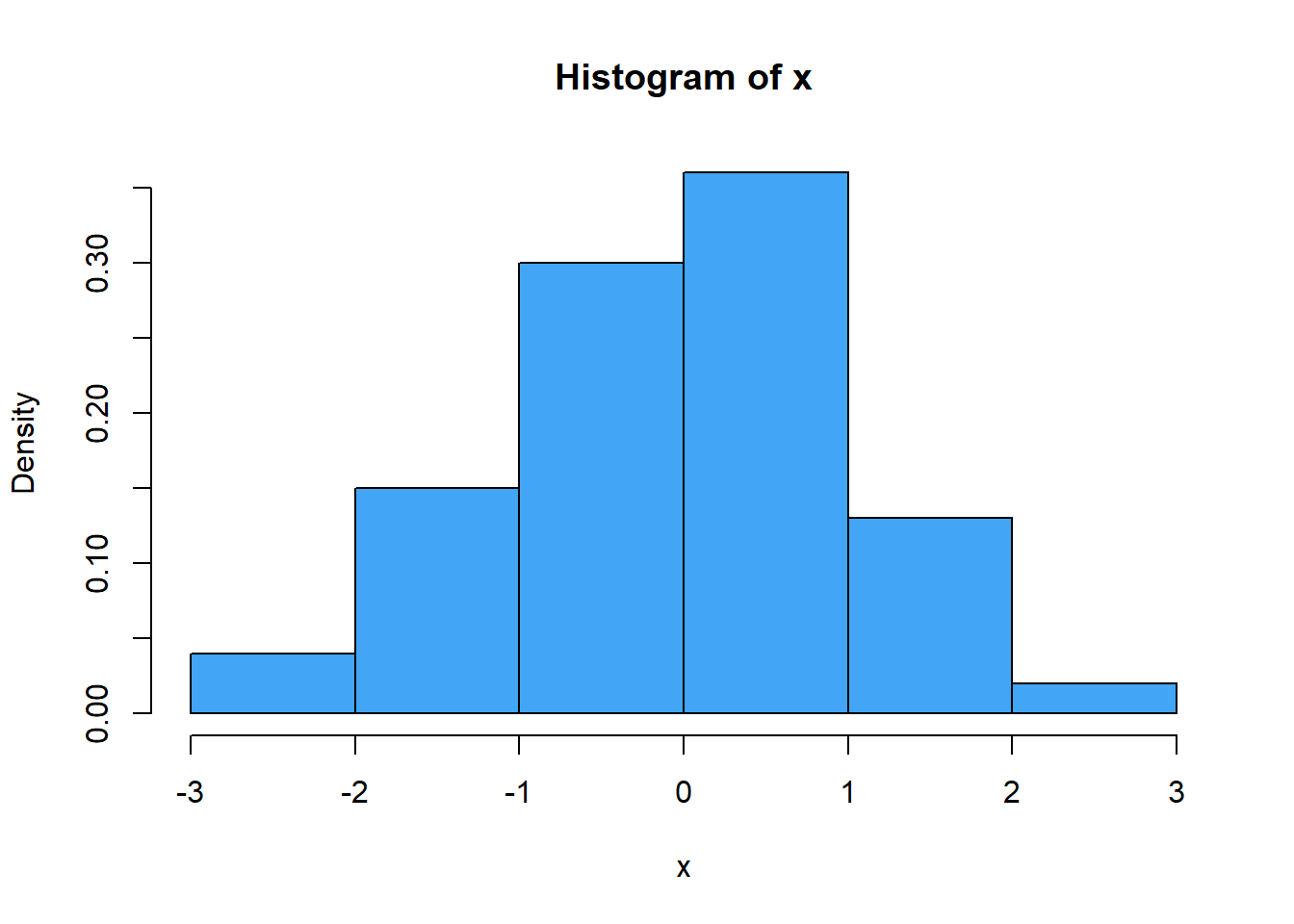
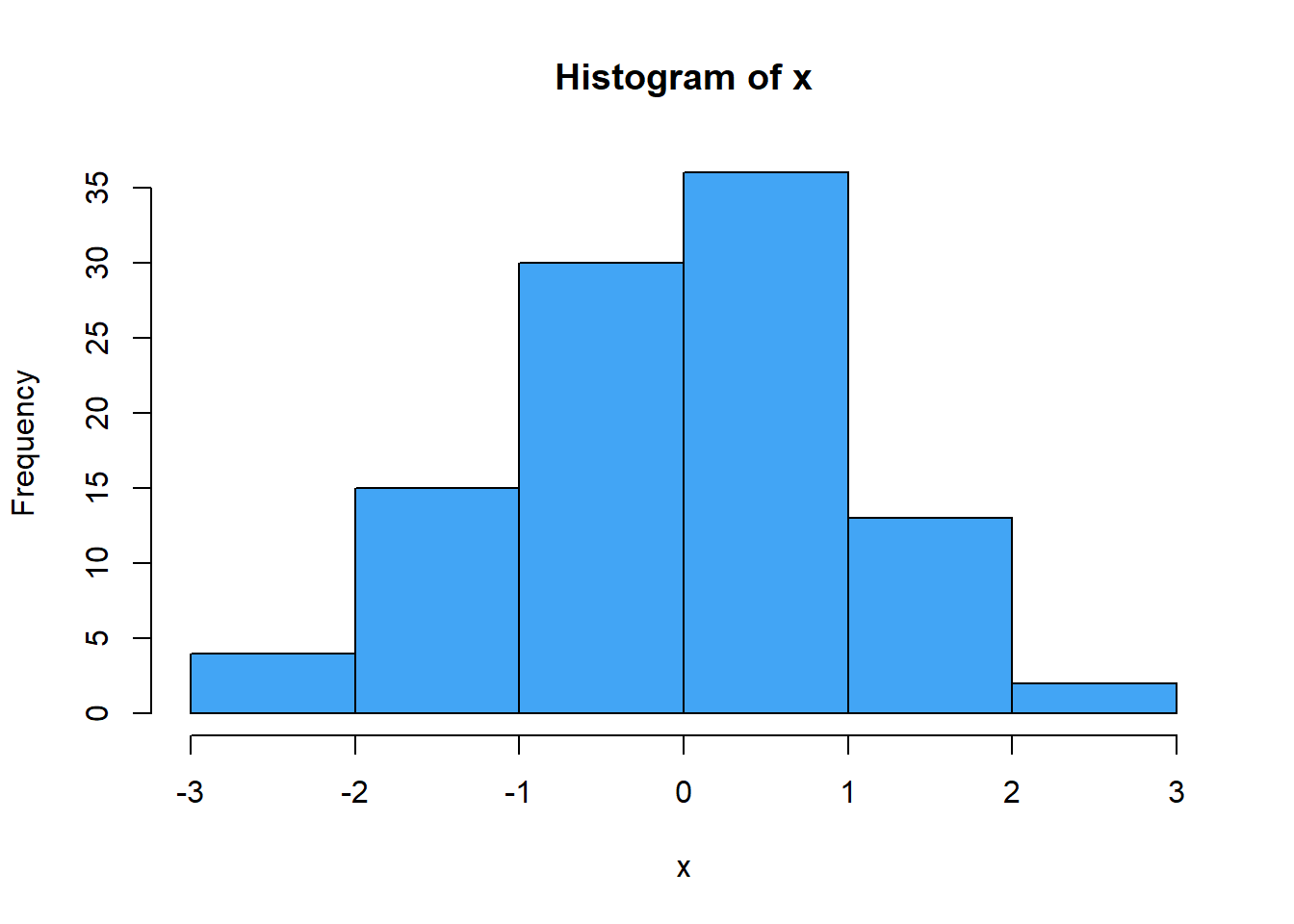
El primer enfonque es realizar la estimación de la función de densidad usando la estimación histograma de la densidad. Por ejemplo, si se tienen 100 datos cuyo histograma de frecuencias absolutas está dado por:

x <- rnorm(100, 0, 1)
hist(x, freq=TRUE, col = "#42A5F5")

La estimación histograma de la densidad dados estos 100 datos es el siguiente:

hist(x, freq=FALSE, col = "#42A5F5")

Para realizar la estimación se tiene en cuenta lo siguiente:

$f\left(x\right)$ es la función de densidad asociada a la variable aleatoria $X$
$\hat{f}\left(x\right)$ es la estimación de la función de densidad
$\hat f_H \left(x\right)$ es la estimación histograma de la función de densidad
El área de cada rectángulo del histograma se denota por $f_j$ y depende del número de datos cuyo valor cae en el dicho intervalo y del número total de datos, de tal manera que $f_j = \frac{n_j}{n}$
El área de cada rectángulo también puede verse en términos de la estimación histograma y de la amplitud del intervalo. $\hat{f}_H \left(x\right) \times 2b$ donde $b$ es un valor a la derecha y a la izquierda del centro del intervalo.

Así, se tiene que si la amplitud del intervalo es $2b$, entonces:

\[\frac{n_j}{n} = 2b \hat{f}_H \left(x\right)\] \[\hat{f}_H \left(x\right)=\frac{n_j}{2nb} \hspace{0.5cm} \textrm{donde} \hspace{0.5cm} n_j=\sum_{i=1}^n \mathbf{I}_{\left[x-b, x+b\right]} \left(x_i\right)\] Ahora, según $n_j$ se tiene que:

\[ \begin{align} x-b \leq x_i \leq x+&b\\ -b \leq x_i-x \leq &b\\ -1 \leq \frac{x_i-x}{b} \leq 1 \end{align} \] y por lo tanto

\[n_j = \sum_{i=1}^n \mathbf{I}_{\left[-1,1\right]}\left(\frac{x_i-x}{b}\right)\]

luego, la estimación histograma de la densidad puede escribirse como:

\[\hat{f}_H \left(x\right) = \frac{1}{nb} \sum_{i=1}^n \frac{1}{2} \mathbf{I}_{\left[-1,1\right]}\left(\frac{x_i-x}{b}\right) = \frac{1}{nb} \sum_{i=1}^n K_U\left(u\right)\] donde

\[u = \left(\frac{x_i-x}{b}\right) \hspace{0.5cm} \mathrm{y} \hspace{0.5cm} K_U\left(u\right) = \begin{cases}\frac{1}{2} & -1<u<1 \\ 0 & \text { e.o.c }\end{cases}\] $K_U$ es un kernel uniforme. Es decir, es una función de densidad centrada en $0$ y toma valores de la forma $u$ entre $-1$ y $1$.

Si ahora se supone que la amplitud del intervalo es $b$, entonces se tiene que:

\[\frac{n_j}{n} = b\hat{f}_H \left(x\right)\] \[\hat{f}_H \left(x\right)=\frac{n_j}{nb} \hspace{0.5cm} \textrm{donde} \hspace{0.5cm} n_j=\sum_{i=1}^n \mathbf{I}_{\left[x-\frac{b}{2}, x+\frac{b}{2}\right]} \left(x_i\right)\] de $n_j$ se tiene que

\[ \begin{align} x-\frac{b}{2} \leq x_i \leq x+&\frac{b}{2}\\ -\frac{b}{2} \leq x_i-x \leq &\frac{b}{2}\\ -\frac{1}{2} \leq \frac{x_i-x}{b} \leq &\frac{1}{2} \end{align} \] y por lo tanto:

\[\hat{f}_H \left(x\right)=\frac{1}{nb} \sum_{i=1}^n \mathbf{I}_{\left[-\frac{1}{2},\frac{1}{2}\right]}\left(\frac{x_i-x}{b}\right)=\frac{1}{nb}K_U\left(u\right)\] donde

\[u = \left(\frac{x_i-x}{b}\right) \hspace{0.5cm} \mathrm{y} \hspace{0.5cm} K_U\left(u\right) = \begin{cases} 1 & -\frac{1}{2}<u<\frac{1}{2} \\ 0 & \text { e.o.c }\end{cases}\] en forma general, si la amplitud del intervalo es $ab$ entonces:

\[\hat{f}_H \left(x\right)=\frac{1}{nb} \sum_{i=1}^n \frac{1}{a} \mathbf{I}_{\left[-\frac{ab}{2},\frac{ab}{2}\right]}\left(\frac{x_i-x}{b}\right)=\frac{1}{nb}K_U\left(u\right)\] donde

\[u = \left(\frac{x_i-x}{b}\right) \hspace{0.5cm} \mathrm{y} \hspace{0.5cm} K_U\left(u\right) = \begin{cases} \frac{1}{a} & -\frac{ab}{2}<u<\frac{ab}{2} \\ 0 & \text { e.o.c }\end{cases}\]

Propiedades del estimador histograma

Dado que el estimador histograma de la densidad depende de la amplitud $b$ del intervalo, la idea es escoger el valor de la amplitud que minimice el $\textrm{MSE}$ para así poder encontrar una estimación más exacta de la función de densidad subyacente a la población en cuestión.

\[\begin{align} \textrm{Var}\left[\hat b - b\right] &= \textrm{E}\left[\left(\hat b - b\right)^2\right] - \left(\textrm{E}\left[\hat b - b\right]\right)^2\\ \textrm{Var}\left[\hat b\right] &= \underbrace{\textrm{E}\left[\left(\hat b - b\right)^2\right]}_{\textrm{MSE}} - \underbrace{\left(\textrm{E}\left[\hat b\right]-b\right)^2}_{\textrm{BIAS}^2}\\ \end{align}\]

y despejando, se tiene que:

\[\underbrace{\textrm{E}\left[\left(\hat b - b\right)^2\right]}_{\textrm{MSE}} = \textrm{Var}\left[\hat b\right] + \underbrace{\left(\textrm{E}\left[\hat b\right]-b\right)^2}_{\textrm{BIAS}^2}\]

Notación $O$ y $o$ de Landau

Notación $O$

$\textrm{Big}-O$ es una notación matemática para describir el comportamiento asintótico de una función, cuando su argumento tiende a un valor en particular o al infinito. Su uso en la computación es análogo, se usa para medir la complejidad de los algoritmos; es decir, la cantidad de operaciones que le toma a un algoritmo realizar internamente para arrojar el resultado final dada una entrada particular del algoritmo.

Por ejemplo, cuando un algoritmo es $O\left(n^2\right)$, se dice que es cuadrático en tiempo y se sabe que estaría en el orden de realizar $n^2$ operaciones para procesar una entrada de tamaño $n$.

Para una función dada $g\left(n\right)$, $O\left(g\left(n\right)\right)$ se define como sigue:

\[O\left(g\left(n\right)\right) = \left\{f\left(n\right): \textrm{existen constantes positivas} \hspace{0.2cm} c \hspace{0.2cm} \textrm{y} \hspace{0.2cm} n_0 \hspace{0.2cm} \textrm{tales que} \hspace{0.2cm} 0 \leq f\left(n\right) \leq cg\left(n\right) \hspace{0.2cm} \forall \hspace{0.2cm} n \geq n_0 \right\}\] Esto quiere decir que $O\left(g\left(n\right)\right)$ es un conjunto de funciones que después de $n_0$ son más pequeñas o a lo sumo iguales que $g\left(n\right)$.

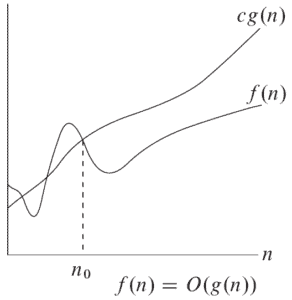
En este gráfico, $f\left(n\right)$ es solo una de las posibles funciones que pertenecen al conjunto de funciones $O\left(g\left(n\right)\right)$. Antes de $n_0$, $f\left(n\right)$ no siempre es más pequeña que $g\left(n\right)$, pero después de $n_0$ nunca sobrepasa a $g\left(n\right)$.

El signo $\left(=\right)$ en la expresión $f\left(n\right)=O\left(g\left(n\right)\right)$ es una representación asintótica la cuál da a entender que cuando $n$ se hace muy grande, $f\left(n\right)$ y $g\left(n\right)$ crecen a la misma velocidad.

Por ejemplo, $3n^3=O\left(n^3\right)$ mientras que $3n\ne O\left(n^3\right)$.

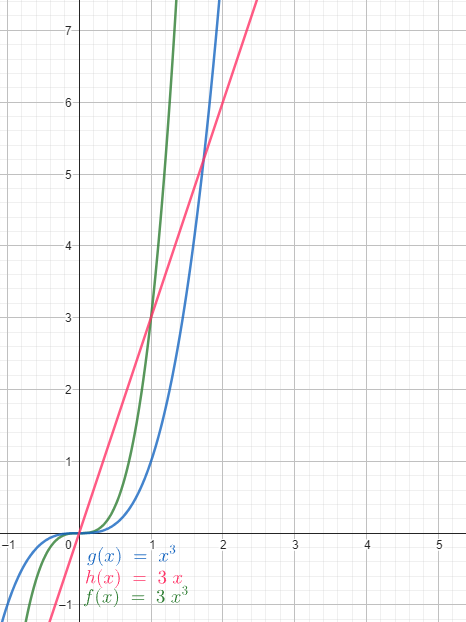
Para verificar que $f\left(n\right) = O\left(g\left(n\right)\right)$, debe existir al menor una constante $c$ con la cuál se cumpla la siguiente desigualdad: \[\left|f\left(n\right)\right|\leq c\left|g\left(n\right)\right| \hspace{0.2cm} \forall \hspace{0.2cm} n \geq n_0.\]

Notación $o$

La notación $o$ es usadapara denotar una cota superior que no es asintóticamente “ajustada”, o sea es estrictamente menor.

Para una función dada $g\left(n\right)$, $o\left(g\left(n\right)\right)$ se define como sigue:

\[o\left(g\left(n\right)\right) = \left\{f\left(n\right): \textrm{para cualquier constante postivia} \hspace{0.2cm} c, \hspace{0.2cm} \textrm{existe una constante positiva} \hspace{0.2cm} n_0 \hspace{0.2cm} \textrm{tal que} \hspace{0.2cm} 0 \leq f\left(n\right) < cg\left(n\right) \hspace{0.2cm} \forall \hspace{0.2cm} n \geq n_0 \right\}\] En esta definición, el conjunto de funciones $f\left(n\right)$ son estrictamente más pequeñas que $cg\left(n\right)$, por lo cuál la notación $o$ es una cpta superior más fuerte que la notación $O$.

La notaci;on $o$ no permite que la función $f\left(n\right)$ tenga la misma velocidad de crecimiento que $g\left(n\right)$.

Esto significa que a medida que $n$ se hace grande, $f\left(n\right)$ se vuelve insignificante respecto a $g\left(n\right)$, es decir:

\[\lim_{n \to \infty} \frac{f\left(n\right)}{g\left(n\right)} = 0\]

En la definición de la notación $o$, la desigualdad debe cumplirse para cualquier constante $c$, mientras que en la notación $O$, es suficiente que algún $c$ satisfaga la desigualdad.
Haciendo una analogía con números reales $a$ y $b$ es algo así como: $f\left(n\right)=O\left(g\left(n\right)\right) \approx a\leq b$ mientras que $f\left(n\right)=o\left(g\left(n\right)\right) \approx a < b$.

Ejemplos

Comprobar si $3x^2 + 25 = O\left(x^2\right)$

\[\begin{align*} & 3x^2 + 25 \leq 3x^2 + 25x^2\\ & \left|3x^2 + 25\right| \leq \left|28x^2\right|\\ & \left|3x^2 + 25\right| \leq 28\left|x^2\right|, \hspace{0.2cm} x>1. \end{align*}\]

en este caso, es como si $c = 28$ y $n_0 = 1$.

Comprobar si $2x^9 + 1 = o\left(x^{10}\right)$

\[\begin{align*} \lim_{x \to \infty}\frac{f\left(x\right)}{g\left(x\right)} &= \lim_{x \to \infty}\frac{2x^9 + 1}{x^{10}}\\ &= \lim_{x \to \infty} \frac{2x^9}{x^{10}} + \frac{1}{x^{10}}\\ &= 0 \end{align*}\]

Serie de Taylor

La serie de Taylor de una función real o compleja $f\left(x\right)$ infinitamente diferenciable en el entorno de un número real o complejo $a$ es la siguiente serie de potencias:

\[f\left(x\right) = f\left(a\right) + \frac{f^\prime\left(a\right)}{1!}\left(x-a\right) + \frac{f^{\prime\prime}\left(a\right)}{2!}\left(x-a\right)^2 + \frac{f^{\prime\prime\prime}\left(a\right)}{3!}\left(x-a\right)^3 + \cdots + \frac{f^{\left(n\right)}\left(a\right)}{n!}\left(x-a\right)^n + \cdots\]

Si $f\left(x\right)$ en diferenciable $n$ veces en torno a $a$, entonces:

donde $R_{n,a}\left(x\right)$ es el residuo de orden $n$ o error de aproximación.

\[R_{n,a}\left(x\right) = \frac{f^{\left(n+1\right)}\left(c\right)}{\left(n+1\right)!}\left(x-a\right)^{n+1} \hspace{0.2cm} \textrm{para algún} \hspace{0.2cm} c \hspace{0.2cm} \textrm{entre} \hspace{0.2cm} a \hspace{0.2cm} \textrm{y} \hspace{0.2cm} x.\] En este caso, la notación $O$ estudia el comportamiento de la función $f$ alrededor de un punto $\left(a\right)$. Se define entonces que $f\left(x\right)=O\left(g\left(x\right)\right)$ si existe $\varepsilon > 0$ y una constante $x > 0$ tal que $|x| implique que $\left|f\left(x\right)\right| \leq c\left|g\left(x\right)\right|$.

Así, $f\left(x\right)$ puede escribirse como:

Volver arriba

Capítulo 1 del curso

Estimación histograma de la densidad

Propiedades del estimador histograma

Notación \(O\) y \(o\) de Landau

Notación \(O\)

Notación \(o\)

Ejemplos

Serie de Taylor